QLU ACM-ICPC大学生程序设计迎新赛-正式赛【解题报告】

发表于 | 更新于 | 分类于

前言：

再次作为吃瓜群众围观4小时，之前一直作为参赛选手参加比赛，从来没想到边缘ob也可以如此精彩。这次还和swt一起“解说”了这场比赛，感觉好有意思，解说真好玩.jpg

因为赛中L题数据出了问题，所以最后一直没人能AK，赛后rejudge时发现崔健聪其实早就在比赛过去$\frac{3}{4}$时AK了，而柳总是第一个过L的，宋健、刘陶然也都1A了。

此次比赛共13题，去掉最后一道直接输出答案的，还剩12道，正好请3位现场AK的队员分工写了下题解，这样我只需要整理一下，不用亲自去做每个题了hhhhh，在此表示一下感谢（づ￣3￣）づ╭❤～。

题解：

崔健聪：A、B、C、D

A、约数个数

题目大意：

输入$n$和$g$，$g$是一个质数，输入$n$行表示$n$个质数$p_1 \ldots p_n$，输入$n$行表示$n$个质数的幂次$ a_1 \ldots a_n$，构成一个$num = p_1^{a_1} \times p_2 ^ {a_2} \ldots p_n^{a_n}$，问你$num$的约数中有多少可以被$g$整除。

解题思路：

因为$g$是质数，所以如果所给的$p$没有$g$那么就不会存在能被$g$整除的$num$的约数，有$g$的话，就是一个排列组合问题。除了$p_i == g$的那个质数外，其余被分解出来的质数都可以取$0$ ~ $a_i$个，所以最后的结果就是：

$a_i（p_i == g）\times (a_1 + 1) \times (a_2+1) \times \ldots \times(a_{i-1} + 1) \times (a_{i+1} + 1) \times \ldots \times (a_{n}+1)$。

Code：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;

const int maxn = 1e5 + 1e2;
int p[maxn];
int a[maxn];
int cnt[maxn];
int main()
{
    int n,g;
    scanf("%d%d",&n,&g);
    for(int i = 1;i <= n;++i)
        scanf("%d",&p[i]);
    memset(cnt,0,sizeof(cnt));
    for(int i = 1;i <= n;++i)
    {
        scanf("%d",&a[i]);
        cnt[p[i]] = a[i];
    }
    if(cnt[g] == 0)
        printf("0\n");
    else
    {
        ll ret = cnt[g];
        for(int i = 1;i <= n;++i)
        {
            if(p[i] == g)continue;
            ret *= (ll)(a[i] + 1);
        }
        printf("%lld\n",ret);
    }
    return 0;
}

B、Alice and Bob

题目大意：

输入n表示有n堆数，输入n个数，表示数的大小。

游戏规则，Alice先手，Bob后手，先手后手轮流取，一次只能拿光一堆数，最后所得到的数的和最大者获胜。

解题思路：

为了获胜，Alice和Bob肯定都从当前所有数中拿最大的。

所以排序，Alice拿偶数位，Bob拿奇数位，计算sum1，sum2，比较输出即可。

局面只有平局和Alice胜利。

Code：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;

const int maxn = 1e5 + 1e2;
int cnt[maxn];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i = 1;i <= n;++i)
        scanf("%d",&cnt[i]);
    ll sum1 = 0,sum2 = 0;
    sort(cnt+1,cnt + n + 1);
    for(int i = n;i >= 0;--i)
    {
        if((n - i) % 2 == 0)
        {
            sum1 += cnt[i];
        }
        else
        {
            sum2 += cnt[i];
        }
    }
    if(sum1 == sum2)
        printf("again\n");
    else
        printf("A\n");
    return 0;
}

C、黑白黑

题目大意：

两种选择，少数为败，存在平局。

输出平局aha或者失败的名字。

解题思路：

if判断就好吧。

Code：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
#define read(n) scanf("%d",&n);
#define readll(n) sacnf("%lld",&n);
const int maxn = 1e4 + 1e3;

int main()
{
    int a,b,c;
    scanf("%d%d%d",&a,&b,&c);
    if(a == b && b == c){
        printf("aha\n");
    }
    else if(a == b)
    {
        printf("C\n");
    }
    else if(a == c)
    {
        printf("B\n");
    }
    else if(b == c)
    {
        printf("A\n");
    }
    return 0;
}

D、GPA

题目大意：

输入7门成绩和对应的学分，给你平均绩点的计算方法，根据该方法进行计算即可。

解题思路：

浮点运算，输出两位小数。

Code：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
#define read(n) scanf("%d",&n);
#define readll(n) sacnf("%lld",&n);
const int maxn = 1e4 + 1e3;
int cost[100];
int fen[100];
double getfen(int x)
{
    double ret;
    if(x >= 91)ret = 4.0;
    else if(x >= 86)ret = 3.5;
    else if(x >= 81)ret = 3.0;
    else if(x >= 76)ret = 2.5;
    else if(x >= 71)ret = 2.0;
    else if(x >= 66)ret = 1.5;
    else if(x >= 60)ret = 1.0;
    else ret = 0;
    return ret;

}
int main()
{
    for(int i = 1;i <= 7;i++)
    {
        scanf("%d",&cost[i]);
    }
    int sum = 0;
    for(int i = 1;i <= 7;i++)
    {
        scanf("%d",&fen[i]);
        sum += fen[i];
    }
    double ret = 0;
    for(int i = 1;i <= 7;i++)
    {
       ret += getfen(cost[i]) * 1.0 * fen[i];
    }
    ret = ret / (sum * 1.0);
    printf("%.2lf\n",ret);
    return 0;
}

刘陶然：E、F、G、H

E、are you ok?

题目大意：

给你一个数据的数目大小 n ($2 <= n <= 100$)，然后给你两行数据，每行有n个，第一行每个数据是字符串（长度不超过10），第二行是对应字符串的个数，拿样例来说，代表apple这个字符串有0个，milk这个字符串有2个。

当所有的字符串的个数为0时就输出are you ok?，否者就出数目不为0 的字符串与其对应的数目。

解题思路：

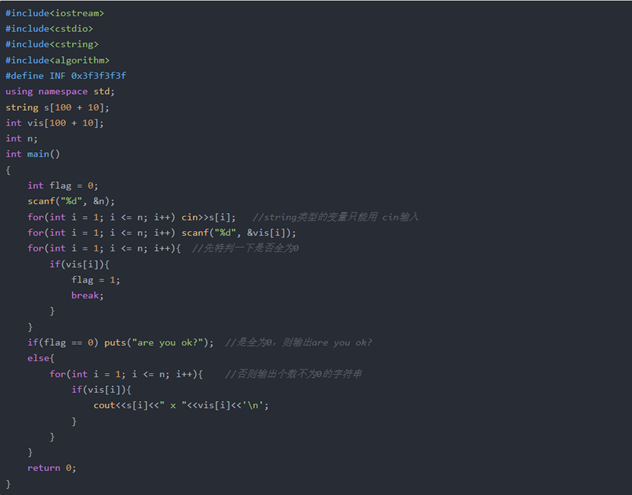
可以用两个数组分别保存字符串还有相应字符串对应的数字，先特判一下是否都为0，是就输出are you ok?否者就按顺序输出字符串的数目不为0的那些。

Code：

F、折纸达人

题目大意：

先输入一个数代表有几组样例($1<= t <= 100$)，对于每组样例，第一行是有几个操作数($1<=n<=10^5$)（L,R,T,B L表示从左向右折……）一个字幕为一次操作，第二行就是给你说具体的操作了，第三行是询问，共四种询问LR, RL, TB, BT，LR表示从左向右剪,依次类推。（Left，Right ，Top ，Bottom）。

解题思路：

​ 你可以先拿一张纸出来，你会发现往左与往右折是一回事，同样往上往下也是，就是左右对折一下或者上下对折一下。从左往右还有从右往左剪开也是一样的，同理上下减也一样。所以问题就是说：左右折几下，上下折几下，然后问你上下剪，或者左右剪开之后有几张纸。

​ 可以再想一下，咱们先就针对上下剪的情况进行讨论一下：

​ 仅上下对折的情况：你会发现你上下对折无数次，剪开仅剩下两张纸。（其实想明白了上下对折对上下剪，没有任何影响,想不明白没关系，继续看）。

​ 仅仅左右对折的情况：你会发现对折0次的时候剪开是$1+1$张，对折1次剪开是$2+1$张，对折3次剪开是$4+1$张，对折4次是$8+1$张，……（大家可以动手试一下）对折n次是$2^n + 1$张。

​ 即上下对折也左右对折的情况：你会发现只要是你是上下剪开的和你上下对折多少次都没有关系（你可以试一下，你会发现你上下对折影响的其实就是，你还是折下看下把，试一下都明白了）。

​ 所以总结规律当你上下剪的时候只需要看左右对折的次数，$剪开纸的数目==2^n + 1$ 张。 同理当你左右剪的时候，只需要看上下对折的次数，规律一样。

Code：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#define INF 0x3f3f3f3f
//大家设置int类型最大值的时候可以设置为这个数，将近int类型最大数的一半，而且乘2还不会爆int
//(这里好像用不到，习惯了，一般都会打上)
using namespace std;
typedef long long ll;
int T;
ll lr, tb;
//这里用快速幂写了一下，算帮大家复习一下了。
//其实for循环也可以过，因为n最大10^5，所以不会超时。
//但是最好不要用c/c++自带的pow(a, b),他会损失精度，int类型的也会损失导致结果错误。
ll power(ll a, ll b)  
{
    ll ans = 1, base = a;
    while(b != 0){
        if(b&1 != 0){
            ans = base * ans % 1000000007;
        }
        base = base * base % 1000000007;
        b >>= 1;
    }
    return ans;
}
int main()
{
    scanf("%d", &T);
    while(T--){
        lr = 0;
        tb = 0;
        ll n; scanf("%lld", &n);
        string c;
        cin>>c;
        for(int i = 0; i < n; i++){
            //统计一下左右折 与 上下折的次数
            if(c[i] == 'B' || c[i] == 'T') tb++;
            else lr++;
        }
        string s;
        cin>>s;
        if(s == "TB" || s == "BT" ){
            printf("%lld\n", ( power(2, lr) + 1 )% 1000000007 ); 
            //结果输出之前记得再模一下，有可能加1正好等于1000000007，那就尴尬了。
        }
        else{
            printf("%lld\n", ( power(2, tb) + 1 )% 1000000007 );
        }
    }
    return 0;
}

G、数数

题目大意：

题意题目描述说的比较清楚了，这里就不在赘述了，简单说就是给你一个串，按照规则翻译成一个别的串，规则题目说的很清楚。

解题思路：

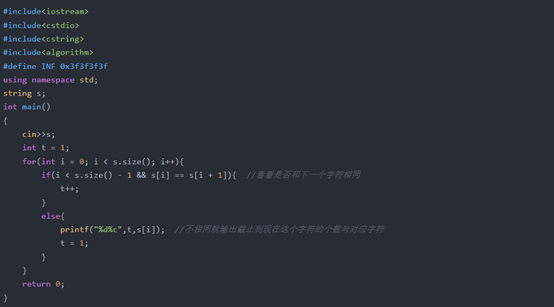
把这个串存起来，然后从头往后找，看有几个连续的，如果就它自己连续，那么输出1x，x就是对应的字符，如果连续n个为它就输出nx。

Code：

H、神奇老虎机

题目大意：

先给你一个样例的个数，然后对于每一个样例，第一行轮子的个数n（$1<=n <=1000$），第二行为n个整数（$1 <= 每个数大小 <= 100$），他让你每组输入对应一行输出，输出字典序最小时老虎机滚轮上显示的数字

解题思路：

​ 贪心，你让每个轮子的字典序都最小，那么整个字典序不就最小么？其实不是这样的，如果让每个轮子的字典序最小，那么又因为每个轮子上数据的范围都是大于等于1的，所以让所有的轮子都直接是1就可以了吗？
​ 你会发现假设给你3个数：
​ 2 20 9 这三个数对应是每个轮子上面最大的数，那么由这三个轮子组成的最小字典序是 1 1 1 吗？ 1 10 1 是不是比 1 1 1 这个字典序更小了，所以呢。除了最后一个轮子，前面的轮子，如果:
​ 当$1 <= a_i <= 9$时，那么该轮子字典序应取1。
​ 当$10 <= a_i <= 99$时 那么该轮子字典序应取10
​ 当$a_i == 100​$时 那么该轮子字典序应取100
​ 但是要注意最后一个轮子，由于它规定了(220的字典序比22的大，因为22是220的一个前缀)所以最后一个轮子一定要是1，才可以保证字典序最小。

举个栗子：
样例输入：

1
6
2 9 11 59 100 63

那么其最小字典序应该对应为：

1 1 10 10 100 1

你可以试一下，不会有比这个更小的了，如果不理解可以找找看有没有比它更小的，找一下，你就理解了。

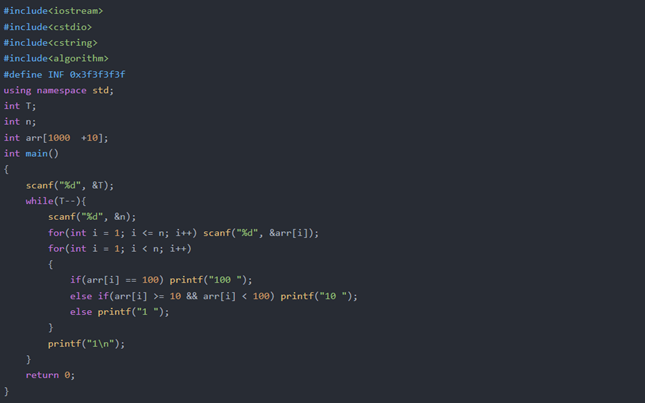
Code：

宋健：I、J、K、L

I、五环

题目大意：

输入一个串，输出一个串；

解题思路：

可以用if else 暴力来做，或者采用Map；

map<string,string>_map;

Code：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
#include<cstdio>
#include<map>
using namespace std;
map<string,string>T;
int main()
{
    T["Blue"]="Europe";
    T["Europe"]="Blue";
    ////
    T["Yellow"]="Asia";
    T["Asia"]="Yellow";
    ////
    T["Black"]="Africa";
    T["Africa"]="Black";
    ////
    T["Green"]="Oceania";
    T["Oceania"]="Green";
    ////
    T["Red"]="America";
    T["America"]="Red";
    string sh;cin>>sh;
    cout<<T[sh]<<endl;
}

J、开挂的小洋

题目大意：

给你N个地鼠出现的时间，在一秒钟最多砸死两个地鼠。求在m时间内最多可以砸死多少只地鼠；

解题思路：

可以定义一个vis数组记录第i秒内出现的地鼠的数量，ans记录最后的结果。

Code：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include<iostream>
#include<cstdio>
using namespace std;
#define maxn (int)1e5+100
int vis[maxn];
int main()
{
    int n,m;cin>>n>>m;
    long long ans=0;
    for(int i=0;i<n;i++)
    {
        int x;scanf("%d",&x);
        if(vis[x]<2)
        {
            vis[x]++;
            ans++;
        }
    }
    cout<<ans<<endl;
}

K、数字匹配

题目大意：

给你一个长度为n的a数组和长度为n的b数组，求两者匹配之后求和的最大和最小；

解题思路：

先对两者进行排序，a最大的乘以b最大的为最大；

maxx=sum(a[i]*b[i])，a,b都是从小到大排序，a最小的乘以b最大的为最小；

Minn=sum(a[i]*b[i])，a从小到大排序，b从大到小排序。

下证：

强强联合，弱弱联合

负数的时候也符合此规律

可以参考白皮书P126页、

Code：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define maxn 1000+100
int a[maxn];
int b[maxn];
int main()
{
    int n;cin>>n;
    for(int i=0;i<n;i++)scanf("%d",&a[i]);
    for(int i=0;i<n;i++)scanf("%d",&b[i]);
    sort(a,a+n);sort(b,b+n);
    int ans1=0,ans2=0;
    for(int i=0;i<n;i++)ans1+=a[i]*b[i];
    for(int i=0;i<n;i++)ans2+=a[i]*b[n-1-i];
    printf("%d %d\n",ans1,ans2);
}

L、寄蒜几盒

题目大意：

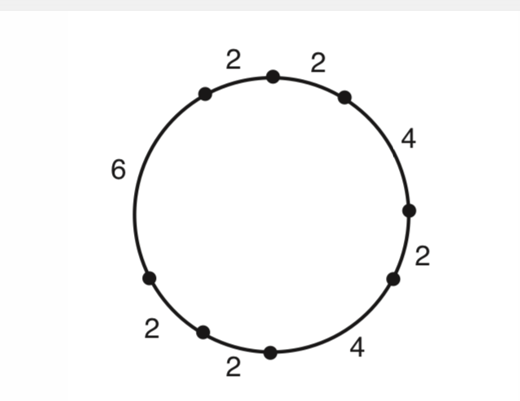
输入一个n;然后输入n段距离，表示第1个点与第2个点之间圆弧的长度、第2个点与第3个点之间圆弧的长度······第n个点与第1个点之间圆弧的长度。

解：转化问题求在n条线段，分成三段完全相等的线段。

解题思路一：

参考白皮书P146。

开2倍的数组，能够实现以任意点为起点的一个环。

尺取：定义c为环的长度/3。

以1为起点开始尺取，取s为头，t为结尾后的第一个节点。

定义sum为第一段的长度，因为环的长度为3*c，若尺取的第一段长度等于c,这时特判从t（t为第一段之后的第一个节点）向后加一直到大于等于c，若有等于c的情况，说明第一段和第二段都满足c，此时可以输出yes；

若此时的第一段长度大于c，则sum减去s的长度，s++;

若s>n，则表示以1到n的节点为头指针的每一段，都不满足情况，输出no;

Code1：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
#include<cstdio>
using namespace std;
typedef long long ll;
int a[(int)1e7+1000];
int main()
{
    int n;scanf("%d",&n);
    int sum=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        sum+=a[i];
        a[n+i]=a[i];
    }
    if(sum%3!=0)puts("No");
    else
    {
        int c=sum/3;
        int s=1,t=1,sum=0;
        bool flg=0;
        while(1)
        {
            while(sum<c)
                sum+=a[t++];
            if(sum==c)
            {
                int temp=t;
                int ff=0;
                while(ff<c)ff+=a[temp++];
                if(ff==c)
                {
                    flg=1;
                    break;
                }
            }
            sum-=a[s++];
            if(s>n)
                break;
        }
        if(flg==1)puts("Yes");
        else puts("No");
    }
}
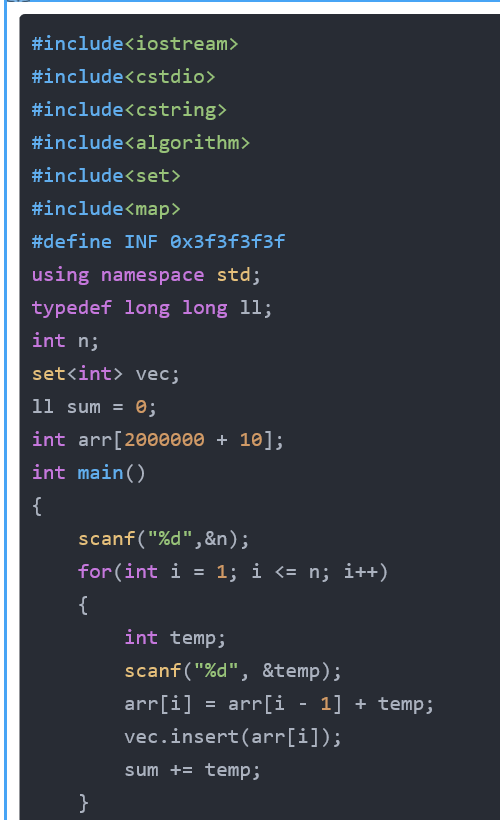
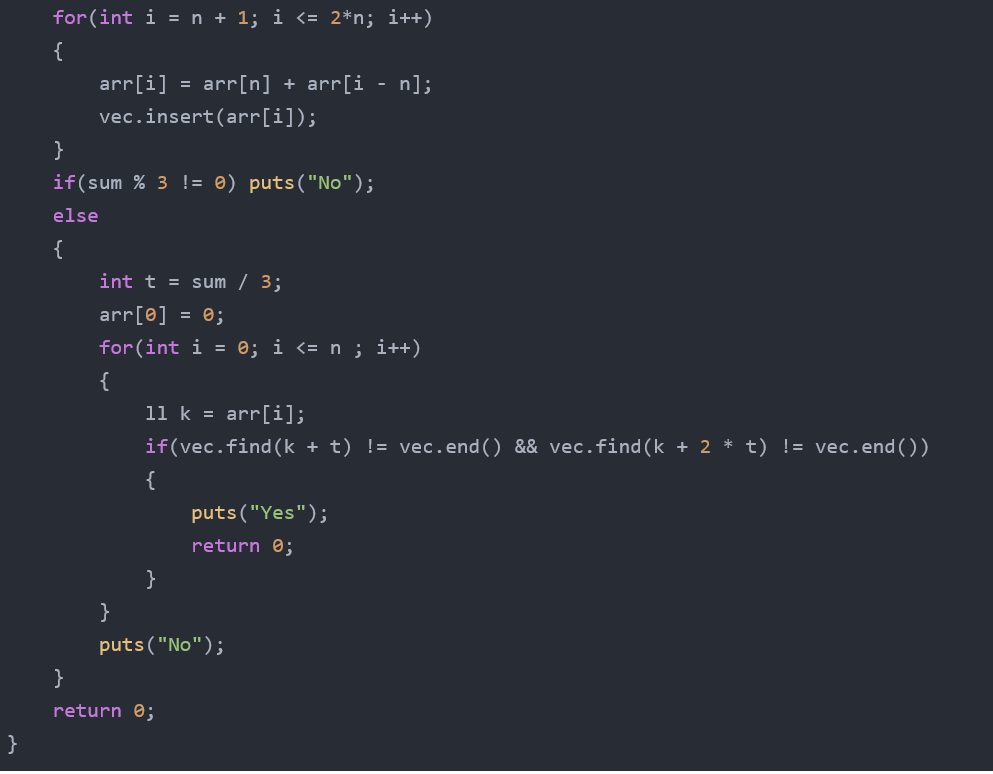
解题思路二：

n的数据范围为1e6 ，每个数据从(1，1000)相乘不会爆int，可以用set集合存数据，二分来取数据（三个点），看是否成立。

可以把环看出一条循环的线，从坐标0出发，第一个点的坐标为0+a[1],第二个坐标为0+a[1]+a[2]……

因为是循环的一个环，所以要增加一倍的坐标放入set容器里，然后用set容器的find函数进行查找；

定义c为环长度的1/3；

从每一个点开始，例如d坐标 ,查找d+c ,d+2*c的坐标是否存在。

若存在，则输出yes,否则以下一个点为起点继续查找，一直找不到输出no;

Code2：

某不愿透露姓名的帅哥：M

M、签到题

题目大意：

略。

解题思路：

略。

Mycode：

略。

碎碎念：

三位队员都给我发的word文档！！而且仅有一位主动附了代码。。Markdown这么好用为啥不用啊喂，好多公式还要手动调整(╯‵□′)╯︵┻━┻(没想到整理出来也用了1h+)。用word就用word吧，代码还以图片的形式放到里面…emmm…后面是不是该安利一波Markdown了。

Donate comment here
0%