题意

求给定子串的最长回文子串。

思路

想法1：枚举每个位置作为回文中心时的情况，往两边扩展看能扩展到什么位置，同时记录长度。时间复杂度$O(n^2)$。
想法2：以前当模板直接用的Manacher算法就是直接用来解决回文串的相关问题的，时间复杂度$O(n)$。（实际上这才是第一眼见到这题想到的想法）

代码

class Solution {
public:
    string longestPalindrome(string s) {

        if(s.size() == 0)   return "";

        char Ma[2020];
        int l = 0, len = s.size(), Mp[2020];
        memset(Ma, 0, sizeof(Ma));
        memset(Mp, 0, sizeof(Mp));

        Ma[l++] = '$';
        Ma[l++] = '#';
        for(int i = 0; i < len; ++i)
        {
            Ma[l++] = s[i];
            Ma[l++] = '#';
        }
        Ma[l] = '0';
        int mx = 0, id = 0;
        for(int i = 0; i < l; ++i)
        {
            Mp[i] = mx > i ? min(Mp[id * 2 - i], mx - i) : 1;
            if(i - Mp[i] < 0)   continue;
            while(Ma[i + Mp[i]] == Ma[i - Mp[i]])   Mp[i]++;
            if(i + Mp[i] > mx)
            {
                mx = i + Mp[i];
                id = i;
            }
        }

        int res = 0, c;
        for(int i = 0; i < 2 * len + 2; ++i)
        {
            if(Mp[i] - 1 > res)
            {
                res = Mp[i] - 1;
                c = i;
            }
        }

        string ans = "";
        for(int i = c - res; i <= c + res; ++i)
            if(Ma[i] != '#')
                ans.push_back(Ma[i]);

        return ans;
    }
};

总结

Manacher算法

步骤：

字符串的转换。
- 方法：添加字符串中原本不存在的符号，如$、#。转换后字符串的长度变为2n + 2。
- 目的：统一奇数长度和偶数长度的回文，给所有子串一个中心。
- 举例：abaaba经转换后在Ma里的情况如下表所示。
- 注意：其中在最开头的位置添加的$免去了字符串是否到达了最左边的判断，减少了代码量。结尾不用加是因为末尾自动有个'\0'。

回文半径的扩展。
- 定义：以当前位置字符为中心向两边扩展，最长的回文串的半径的长度。
- 举例：abaaba对应的回文半径的长度在Mp里的情况如下表所示。
- 注意：Mp[i] - 1对应了原串的回文子串长度，Ma[i - Mp[i] ~ i + Mp[i]]是回文串。

核心

如何在$O(n)$时间内求出Mp数组？

符号表示：mx表示i + Mp[i]的最大值，id表示mx的下标。
算法过程：从前往后求Mp数组，同时更新mx和id的值。

假设已经知道了0 ~ i - 1位置上的Mp的值，如何求i位置的Mp的值？
- Case 1，mx > i
  
  j = 2 * id - i是i关于id的对称点，此时i位置的回文半径就可以根据j位置的回文半径与mx的关系直接得出，为min(Mp[j], mx - i)。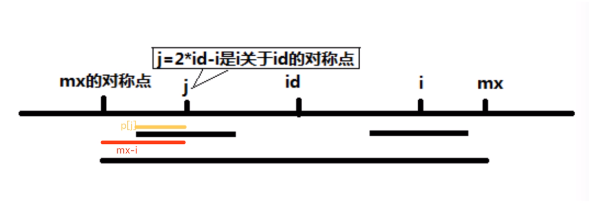
- Case2， mx ≤ i
  
  此时无法用前面已经得到的关系求i位置上的回文半径长度，故设置为1，再以此位置为中心进行扩展得出答案。

代码

void Manacher(char s[], int len)
{
    int l = 0;
    Ma[l++] = '$';
    Ma[l++] = '#';
    for(int i = 0; i < len; ++i)
    {
        Ma[l++] = s[i];
        Ma[l++] = '#';
    }
    Ma[l] = 0;

    int mx = 0, id = 0;
    for(int i = 0; i < l; ++i)
    {
        Mp[i] = mx > i ? min(Mp[2 * id − i], mx − i) : 1;
        while(Ma[i + Mp[i]] == Ma[i - Mp[i]])	Mp[i]++;
        if(i + Mp[i] > mx)
        {
            mx = i + Mp[i];
            id = i;
        }
    }
}

复杂度分析

时间复杂度：$O(n)$。
空间复杂度：$O(n)$。